用MATLAB演示采样频率和点数对FFT的影响

2013.05/Uncategorized

FFT是指离散傅里叶变换的快速算法，可将时域信号变换为频域。

在MATLAB中做FFT，首先编写函数，对不同的采样频率和采样点数，计算FFT后的频率序列及其对应的幅值：

function [f amplitude] = yopheeFFT(sampleRate,FFT_points)
    n = 0:FFT_points-1;
    t = n/sampleRate; %采样时间序列
    f_All = n*sampleRate/FFT_points; %频率序列

    %构造混有噪声的周期信号并采样
    signal = 2*sin(2*pi*10*t)+1*sin(2*pi*20.25*t)+0.2*randn(size(t));

    %对信号进行快速Fourier变换，并求振幅
    amplitude_All = abs(fft(signal,FFT_points))*2/FFT_points;

    f = f_All(1:FFT_points/2);
    amplitude = amplitude_All(1:FFT_points/2);

其中时域信号为幅值2、频率10Hz和幅值1、频率20.25Hz的两个正弦信号和一个噪声信号的叠加。

指定不同的采样频率和采样点数，调用函数做FFT计算，并绘图显示：

sampleRate = 32; %采样频率
FFT_points = 64; %采样点数
[f amplitude] = yopheeFFT(sampleRate,FFT_points);
plot(f,amplitude);

sampleRate = 64;
FFT_points = 64;
[f amplitude] = yopheeFFT(sampleRate,FFT_points);
plot(f,amplitude);

sampleRate = 64;
FFT_points = 512;
[f amplitude] = yopheeFFT(sampleRate,FFT_points);
plot(f,amplitude);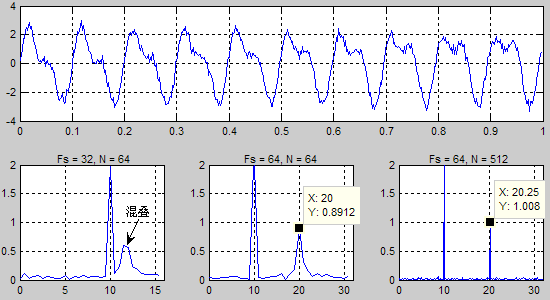

图片上方为时域信号。下左图采样频率低于信号成分最高频率的2倍，未识别出信号中20.25Hz的频率成分，并且出现混叠。下中图频率分辨率为1Hz，将20.25Hz识别为20Hz。

总结：

  • FFT频谱图具有对称性，显示一半即可
  • FFT计算结果乘以2除以采样点数得到真实振幅
  • FFT频率分辨率 ＝ 采样频率 / 采样点数
  • 采样频率应大于信号中最高频率的2倍
京ICP备14036213号-2